前回記事を書いてからだいぶ時間が経ってしまって5月にエントリがひとつもないのもさみしいので、書きかけだった記事をアップしておきます。iPadから書き込んでみたいというのもあったので…。

最近はiPhoneOS4.0にどっぷり使っていまして、あまり書けることがないんですよねぇ。ってことで、フーリエ変換の流れで今回は位相の話です。逆離散フーリエ変換とか行きたいところですが、またの機会にします。

位相とは

これまでの説明で何度か位相という言葉を使ってきたと思いますが、ちゃんとその定義を調べずに使っていたので、改めてwikipediaなどを見てみますと…

位相 (Wikipedia)

「ひとつの周期中の位置を示す無次元量」なんて書いてあって、無次元量って何だ？なんて思ってしまうわけですが、まぁ、DFTで使っているサイン波でいえば、サイン波の中のどの位置かということと思われます。さらに、周期のスタート位置の位相は「初期位相」というそうで、初期位相の事を単純に位相といわれたりすることもある、だそうです。「位相が○度ずれている」と言ったときには、２つの同じ周波数のサイン波を同じ時間軸にならべた状態で「初期位相が○度ずれている」という理解になるかと思います。

サイン関数を使ってサイン波を作る場合などは位相をラジアンで渡して値を取得しますが、0〜2π（角度で表すなら0°〜360°）が一周期で、2π以上や0以下の値を渡しても、返ってくるのは同じ値の繰り返しとなります。たとえば、0から始まるサイン波と、2πや4πや-2πから始まるサイン波というのは、全く同じ形となりますので、同じ位相といえます（たぶん）。DFTの周波数成分は、繰り返されているサイン波の１周期ですので、その位相はどこか2π分の範囲の中の位置だけを考えれば良い事になります。

直線位相特性

よくデジタルフィルタの本をみていると、FIRフィルタだと位相のずれがない直線位相特性のフィルタが実現できるなんて書いてあったりします。下の図が直線位相特性のグラフなのですが…

これを最初見た時は位相がずれないといってるのに、位相が周波数によってずれるというのが僕はよく理解できなかったのですが、いくつかのサイン波を並べて同じ時間遅らせて、遅らせたタイミングでも同じ波形になるようにしてみるとわかります。

上の図では1Hzのサイン波を3/4周期遅らせて、同じ時間2Hzと3Hz遅らせて並べてみています。元のサイン波が緑色で、遅らせたサイン波が青色です。各周波数を同じ時間遅らせているので、遅らせたあとの波形はどの周波数も元の波形と同じ形に保たれます。

1Hzの3/4周期の遅れに対して、2Hzは3/2周期、3Hzは9/4周期、と位相がずれています。このような感じで周波数に比例して位相がずれるというのが直線位相特性です。直線位相特性を実現したフィルタを使用すれば、周波数によって位相のずれがないので、クオリティの高い処理ができるということのようです。

離散フーリエ変換の第２回目という事で、実際にどういうことをやっているのかをコードで見ていきたいと思います。前回のDFTのコードの変換を行っているところが以下の部分です。

// iは抜き出す周波数
for (int i = 0; i < n; i++) {
    
    tmpReal[i] = 0.0;
    tmpImag[i] = 0.0;
    
    // 1サンプルの位相の差分
    double d = 2.0 * M_PI * i / n;
    
    for (int j = 0; j < n; j++) {
        
        double phase = d * j;
        
        // コサインをかけた結果を加算する
        tmpReal[i] += real[j] * cos(phase);
        // マイナスサインをかけた結果を加算する
        tmpImag[i] -= real[j] * sin(phase);
    }
}

変換するオーディオデータに対して、抜き出す周波数のcosをかけ算して全て足し合わせた値が実部、-sinをかけて足し合わせた値が虚部になります。具体的に説明はしませんが、このようにする事で、それぞれの周波数のcosやsinがオーディオデータにどれくらい含まれているかを得る事ができます。（ちゃんと理解したい方は、なにかしらフーリエ変換の本などを参考にしてください）

抜き出す周波数というのは、0Hzから始まって1Hz、2Hz...と続いて、変換するサンプル数-1Hzまでです。つまり、変換するサンプル数と同じ数の周波数成分に分けられます。DFTは、変換するオーディオデータが延々とループしていると仮定して周波数成分を取り出しますので、1Hz以上の周波数はぴったり整数の周波数になります。

上の図を見ると、cosもsinも0Hzの時は横一直線になっています。0HzはDC成分といわれたりしてちょっと特別です。cos0Hzでは全体に1がかけられますので、波形全体がプラスとマイナスのどちらにバランスが偏っているかという要素になります。sinは0をかけているので、元がどんな波形だろうと結果は0になります。

ちなみに、下の図の1.23Hzみたいな中途半端な周波数のサイン波などというのは途中で急激に途切れた状態で繰り返されることになりますので、DFTをすると1Hzを中心に高い周波数まで全体的に成分が含まれることがわかります。

また、ちょっと説明が後回しになりましたが、なぜDFTでcosとsinを抜き出すかといえば、同じ周波数のcosとsinを足し合わせることで、360度どの位相のサイン波でも表現できるからです。

本当にcosとsinの足し算でサイン波が作れるのか、検証してみたのが以下のコードです。stRadを0〜2πの間で変えてみて実行してみてください。sinはDFTと同じようにマイナスにしています。もちろん計算の誤差はあると思いますので、近ければOKという基準で判断すれば、どの位相のサイン波でも、スタート位置がゼロのcosとsinの足し合わせで作り出せる事がわかると思います。（てきとうに書いたので、なんかおかしかったらすみません。0〜2πの範囲外では正確な結果が出るようになってません）いちおうDFTと同じように、sinはマイナスsinでやってます。

#include <stdio.h>
#include <math.h>
int main (int argc, const char * argv[]) {
    
    double stRad = 0.0; //sinの開始位置。0〜2πの間で！
    int n = 16;
    
    double xcos = 0;
    double xsin = 0;
    double co = fabs(sin(stRad));
    double si = sqrt(1.0 - co * co);
    
    if (stRad < M_PI_2) {
        //第一象限
        xcos = co;
        xsin = -si;
    } else if (stRad < M_PI) {
        //第二象限
        xcos = co;
        xsin = si;
    } else if (stRad < M_PI_2 * 3) {
        //第三象限
        xcos = -co;
        xsin = si;
    } else {
        //第四象限
        xcos = -co;
        xsin = -si;
    }
    
    for (int i = 0; i < n; i++) {
        
        double phase = (double)i / n * 2.0 * M_PI;
        double sinVal = sin(stRad + phase);
        double mixVal = cos(phase) * xcos - sin(phase) * xsin;
        
        printf("sin %03d %f / sin+cos %f\n", i, sinVal, mixVal);
        if (fabs(sinVal - mixVal) > 0.000001) {
            printf("error\n");
            return 0;
        }
    }
    
    printf("success\n");
    
    return 0;
}

MacとかiPhoneとかあまり関係なく基礎を固めようと思っていろいろ勉強モードに入っていまして、すこしずつまとめていこうと思います。まずはフーリエ変換についてです。

あくまでプログラムで使う事を前提に書いていきますので、いろいろおかしかったりするかもしれませんがご了承ください。もし、明らかに変だったら突っ込んでいただけるとうれしいです。基本的に小難しそうな数式とかはできるだけ出さずにコード重視、ビジュアル重視で書いていくつもりです。

プログラミングでフーリエ変換というと、高速フーリエ変換（FFT）を使うという事になると思うのですが、FFTについては特に詳しく書きません。プログラム化されたコードを見た場合、FFTだと高速化されたアルゴリズムだけで本質的な部分がわからないので、高速化していないノーマルな離散フーリエ変換（DFT）のプログラムを見て、フーリエ変換の仕組みを調べていきます。

オーディオ信号に対してDFTを使うと何ができるかというと、時間単位で並んでいる時間領域のオーディオデータの一部分を切り出して、含まれている周波数ごとの成分に分けた周波数領域のデータに変換する事ができます。逆に、その周波数領域のデータを時間領域のオーディオデータに戻す事もでき、それが逆離散フーリエ変換（IDFT）になります。

離散フーリエ変換というのは、デジタルでサンプリングされたオーディオ信号のような飛び飛びのデータに対して行うフーリエ変換です。いきなり「離散」と出てくると何の事かわからないかもしれませんが、「離散」＝「デジタル」と考えればよいと思います。アナログの「連続」に対して、デジタルの「離散」です。そのDFTを高速化したのがFFTという関係になります。

まずは何より使ってみない事にはしょうがないということで、サンプルソースです。

#include <stdio.h>
#include <math.h>
void DFT(int n, double *real, double *imag)
{
    double tmpReal[n], tmpImag[n];
    
    for (int i = 0; i < n; i++) {
        
        tmpReal[i] = 0.0;
        tmpImag[i] = 0.0;
        
        double d = 2.0 * M_PI * i / n;
        
        for (int j = 0; j < n; j++) {
            
            double phase = d * j;
            
            tmpReal[i] += real[j] * cos(phase);
            tmpImag[i] -= real[j] * sin(phase);
        }
    }
    
    for (int i = 0; i < n; i++) {
        real[i] = tmpReal[i];
        imag[i] = tmpImag[i];
    }
}
int main (int argc, const char * argv[]) {
    
    int n = 16;
    double real[n], imag[n];
    
    double d = 2.0 * M_PI / n;
    
    for (int i = 0; i < n; i++) {
        real[i] = sin(1.0 * i * d); //1Hzのサイン波
        real[i] += sin(3.0 * i * d + M_PI_4); //3Hzのサイン波（1/4πずらし）
        real[i] += sin(5.0 * i * d + M_PI_2); //5Hzのサイン波（1/2πずらし）
        imag[i] = 0.0;
    }
    
    //フーリエ変換
    DFT(n, real, imag);
    
    for (int i = 0; i < n; i++) {
        printf("%dHz %f\n", i, sqrt(real[i] * real[i] + imag[i] * imag[i]));
    }
    
    return 0;
}

Xcodeで実行する場合はCのCommand Line Toolでプロジェクトを作って、main.cを書き換えてください。

今回のコードでは、1Hzと3Hzと5Hzのサイン波をいろいろ位相を変えてミックスして元のデータを作ってから変換しています。結果は、

0Hz 0.000000
1Hz 8.000000
2Hz 0.000000
3Hz 8.000000
4Hz 0.000000
5Hz 8.000000
6Hz 0.000000
7Hz 0.000000
8Hz 0.000000
9Hz 0.000000
10Hz 0.000000
11Hz 8.000000
12Hz 0.000000
13Hz 8.000000
14Hz 0.000000
15Hz 8.000000

と表示されて、1Hzと3Hzと5Hzが含まれているということがわかります。上の周波数の11Hzと13Hzと15Hzにもデータが現れていますが、これは、ナイキスト周波数以上の周波数の音は、ナイキスト周波数を対称に折り返した低い周波数へ現れるということで出てきているものですので、単純に周波数特性を調べるだけなら無視してください（けっして無意味なデータというわけではありませんが...）。

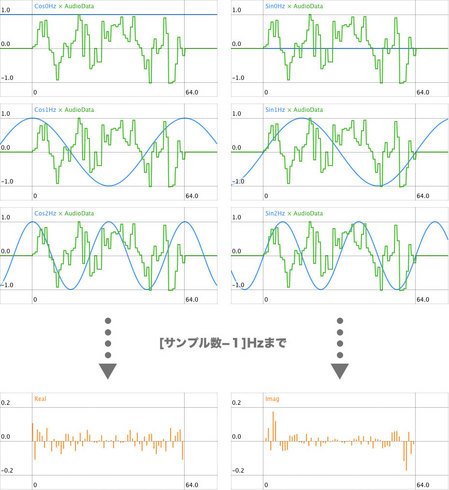
コードの説明に入りまして、DFT関数がまさに離散フーリエ変換する関数になります。realに変換したいオーディオデータの配列、imagに同じサイズの空の配列、nに配列のサイズをそれぞれ渡すと、realとimagにフーリエ変換された値が返ってきます。

DFTをすると１つの周波数ごとにデータが実部と虚部という２つに分かれて返ってきます。今回のコードではrealが実部、imagが虚部のデータです。実部と虚部は２つでひとつの意味を持ったデータですので、どちらかだけを使うことはあまり無いと思います。main関数の中でやっていますが、周波数特性の振幅を得るという場合はrealとimagをそれぞれ２乗した値の平方根を求めます。

DFTして得られる周波数は、DFTに渡すサンプル数の長さを1Hzとして、0からサンプル数-1までの整数倍の周波数です。16サンプルの場合は、0・1・2・3・4・5・6・7・8・9・10・11・12・13・14・15Hzの16個です。ただこれが1
秒を1Hzと考えるときには、たとえば44.1kHzのオーディオの中の64サンプルを変換したという状況だと、0・689・1378...というふうにもっと広い間隔の周波数の並びになります。これはどこを基準にするかで違ってくるというだけの話ですので、このDFTの説明ページでは変換するサンプル数を1Hzとして表現します。

とりあえず、DFTができましたというところで１回目は終わりです。次へつづきます。